1. 実験1:暗黙の知能観がモチベーションを高める仕組み
実験1は、中学校にあがる生徒たちの、知能観と、成績に関係するその他のモチベーション要素を計測し、それらが彼らの7年生と8年生の成績にどのように影響しているかを測定するものです。そして、それらの測定結果から、暗黙の知能観が、どのようにより良い成績に繋がるかという因果関係のモデル(モチベーション経路モデル)を検証します。
1.1. 被験者のデータ
ここから実験の詳細を解説していきます。これらは無理に読み込む必要はありません。基本的にデータの集め方と、分析の統計的根拠について書かれていますので、興味のある方だけ読み進めて頂ければ十分だと思います。
そうでない方は、実験2のはじめまで飛ばしてください。
さて、この実験には、ニューヨーク市の7年生になる373人(女子198人、男子175人)の生徒が参加しています。新入生たちは4年に分けて入学してきました。新入生が最も少ない年は67人で、最も多い年は114人でした。
Table1.の通り、それぞれのグループの中学入学時の平均成績と暗黙の知能観の平均スコアは顕著に異なっています。
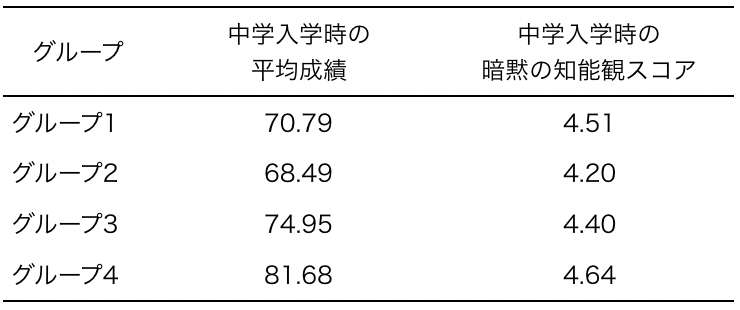
また、被験者の人種や社会背景も様々です。まず55%がアフリカ系アメリカ人、27%が南アジア人、15%がヒスパニック、3%が東アジア人とヨーロッパ系アメリカ人でした。被験者の生徒たちのうち、53%は世帯の収入が低いため無料ランチの利用者です。彼らは、平均よりもよくできる生徒たちで、6年生の時の算数テストの平均点数は、全国の75パーセンタイル(上位25%)に位置しています。
これらの4グループの生徒たちの7年生と8年生の時の2年間の成績が、合計5年に渡って追跡調査されました。
中学入学時の秋学期のはじめに、知能観、ゴール選好、努力に対する信念、失敗に対する習熟指向の反応と救いのない反応などを調査する為に、生徒たちにモチベーションに関するアンケートを埋めてもらいます。
また、実験に先立って、参加生徒たちの6年生の最終学期の算数の成績も得ています。そして、それぞれの年の秋学期と春学期の終わりに、7年生の時と8年生の時の数学の成績を得ます。それぞれのグループで数学の教師は一人だけです。
1.2. 測定項目と測定方法
この研究で測定する項目は、大きく分けて、数学の成績とモチベーション変数の2つです。
1.2.1. 成績
成績の測定科目として、数学を選んでいます。数学は一般的に誰もが困難を経験する科目だからです。そのため、数学は、困難な状況におけるモチベーションのパターンを観察するための要件を満たしていると言えます。
数学は、より難しいレベルの問題を解くには、それまで学んできた公式を組み合わせて活用することが必要です。つまり、数学のスキルは、時間とともに積み重ねていくタイプのものと言えます。そのため、数学の成績は、生徒たちの粘り強い努力の度合いを正確に反映するものと考えられます。
当研究において、生徒たちの数学の成績は、テストの点数、宿題、課題、クラスへの参加度を加味した上で、総合的に算出されます。
なお、数学のテストの測定には、ニューヨーク市が実施している市統一テスト(CAT)を使っています。研究前の指標として6年生の春学期(最終学期)の点数、研究中の指標として7年生の秋学期と春学期、8年生の秋学期と春学期の点数を用います。
数学テストのデータはTable2.の通りです。
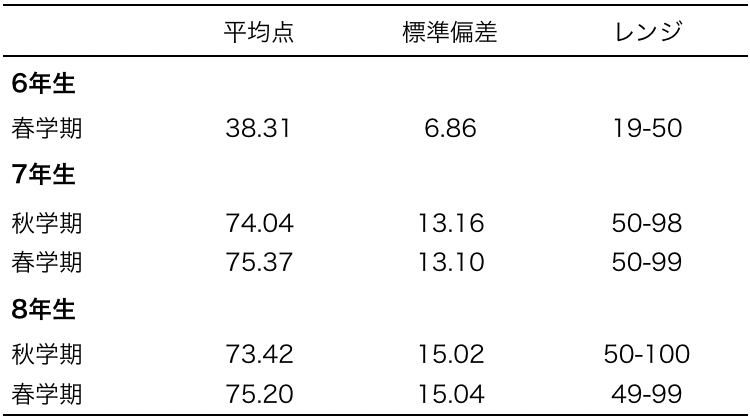
1.2.2. モチベーション変数
成績に影響を与える要員として、5つのモチベーション変数を測定します。
- 暗黙の知能観
- ゴール選好
- 努力に対する信念
- 困難な状況に直面した時の救いのない解釈(現実逃避)の少なさ
- 困難な状況下でポジティブな戦略を模索する傾向
これらのモチベーション変数は、用意された質問に対して、1(強く同意する)から6(強く反対する)の6ポイントスケール(リッカート尺度)をつけるアンケートで測定されます(Table3.)。
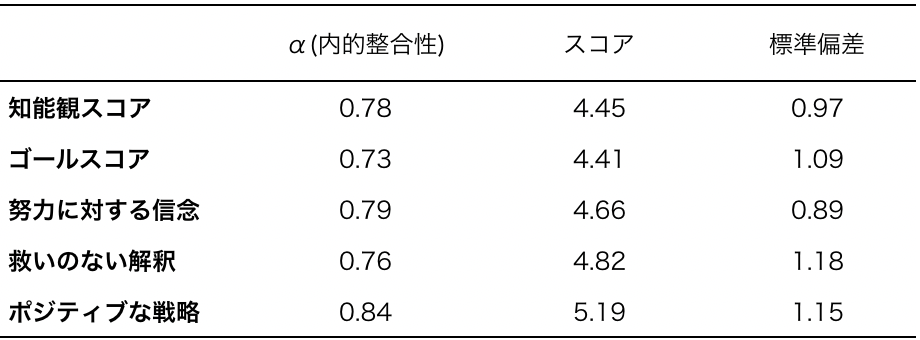
それぞれ解説します。
知能観の測定
知能観を測るアンケートは6問で構成されています。3つは固定的知能観を表す文です(例:「あなたの持って生まれた知能は決まっており、それを変えるためにできることはあまりない」)。3つは暗黙の知能観を表す文です(例:「あなたはいつだって知能を大きく変えられる」)。暗黙の知能観のスコアは反転して測定します。つまり、スコアが低ければ低いほど固定的知能観を持っており、スコアが高ければ高いほど暗黙の知能観を持っているということを表します。
ラーニング・ゴールの測定
ラーニング・ゴールの測定には、ミドグリーらが『生徒たちの達成状況におけるゴール選好の評価スケールの発展と妥当性確認』で開発したPALS(Patterns of Adaptive Leaning Survey)が使われています(※1)。ラーニング・ゴールを表す3つの文、「私が学業をやる最も重要な理由は新しいことを学びたいからだ」、「私は一番考えさせられる学業を最も好む」、「例え沢山間違えたとしても、私は学ぶことができる学業を好む」を用いて測定します。これもスコアが高いほど、ラーニング・ゴールであることを表します。
努力に対する信念の測定
努力に対する信念の測定は、ブラックウェルの『中学校へ上がる生徒たちの達成の心理学的橋渡し役:暗黙の知能観の役割』を参考にしています(※2)。努力の価値を肯定する4つの文(例:「何であれ、努力すればするほど、うまくできるようになる」)と、努力の価値を否定する5つの文(例:「実際、学業で努力しなければいけないとしたら、自分が賢くないのだと思う」)が使われています。努力の価値を否定する文のスコアは反転して計算されます。つまり、スコアが高いほど、努力に対するポジティブな信念を持っていることを表します。
困難な状況における反応パターンの測定
困難な状況に置かれた時の、生徒たちの「救いのない解釈の少なさ」と「ポジティブな戦略を取る傾向」を測定するために、ま図、生徒たちに架空の失敗ストーリーを紹介し、それに対してどう考えるか行動するかを聞きました。
架空のストーリーは次のようなものです。
年初に新しいクラスが始まりました。あなたは、その教科も先生もとても好きです。あなたは、その教科をとてもよく理解していると考えています。そして、最初の小テストのために中程度勉強しました。いくつかは答えが分からなかったとしても、小テストはそれなりに良くできたと思えました。テストの結果が帰ってきました。あなたの点数は54点(落第点)でした。
これに対して、以下の2つのアンケートを行います。
(a)救いのない解釈(現実逃避)の少なさ
失敗の原因を努力不足とする習熟指向の2つの文(「十分に努力して勉強しなかった」「正しい道筋で勉強できていなかった」)と、持って生まれた能力の不足を原因とする救いのない4つの文(「自分は賢くない」「この科目が得意ではない」「テストが意地悪」「この科目が嫌いだ」」が使われました。スコアが高いほど救いのない解釈(現実逃避)が少なく、スコアが低いほど救いのない解釈(現実逃避)が多くなります。
(b)ポジティブな戦略(より良い戦略)を模索する傾向
努力をベースとした戦略(例:「これからクラスでもっと努力する」「テストのための勉強時間を増やす」)と、努力から逃げる戦略(例:「もう二度とこの科目は取らない」「これからこの科目の勉強時間は減らす」「次のテストはカンニングする」)のどちらを採用する傾向があるかが測定されました。スコアが高いほど努力をベースとした戦略を取り、スコアが引くほど努力から逃げる戦略を取ることを表します。
1.3. 結果
1.3.1. 暗黙の知能観とモチベーションの関係
まず、暗黙の知能観の信念をより強く持つ生徒たち、つまり「知能は努力や訓練によって伸ばすことができる」と信じている生徒たちは、あらゆる面でポジティブなモチベーションを持つ傾向があることがわかりました。
つまり、暗黙の知能観と、各種モチベーション要素は正の相関関係(一方が高ければ、他方も高い)にあるということです。(Table4)。

このように、暗黙の知能観はラーニング・ゴールになること(r=.34, p<.01)、努力に対するポジティブな信念を持つこと(r[相関係数]=.54, p<.01)、困難な状況において現実逃避しないこと(r=.44, p<.01)、困難な状況においてより良い戦略を考えること(r=.45, p<.01)と、正の相関関係があることが分かりました。
加えて、モチベーション変数同士も、各々が、お互いに正の相関関係で作用し合っていることがわかりました(rs=.34-.72, p<.01)。つまり、努力に対するポジティブな信念が高い生徒ほど、困難な状況に直面すると、学習方法(戦略)を見直すというように今までの取り組み方を改善しようとします。また、困難な状況で現実逃避しない傾向が高いほど、努力に対するポジティブな信念を持っています。
つまり、将来の達成に大きな影響を及ぼすと考えられる、以下の各種モチベーション要素、
- 暗黙の知能観
- ラーニング・ゴール
- 努力に対するポジティブな信念
- 困難な状況における救いのない解釈(現実逃避)の少なさ
- 困難な状況下でポジティブな戦略を模索する傾向
は、それぞれ相互に密接に繋がっているということです。そして、どれかいずれの要素が高まれば高まるほど、全体としてもモチベーションが高まっていくということです。
1.3.2. 暗黙の知能観と学業成績の関係
次に、困難な状況になればなるほど、暗黙の知能観(能力は努力と訓練によって伸びる)の信念を持つ人は、より高い成績や業績を達成していくことがわかりました。
具体的には、暗黙の知能観と学業成績は、正の相関関係(一方が高ければ他方も高い)にあることがわかりました。この傾向(相関係数)は、生徒たちが中学校でより多くの年数を経るにしたがって、顕著になっていきます(Figure1)。
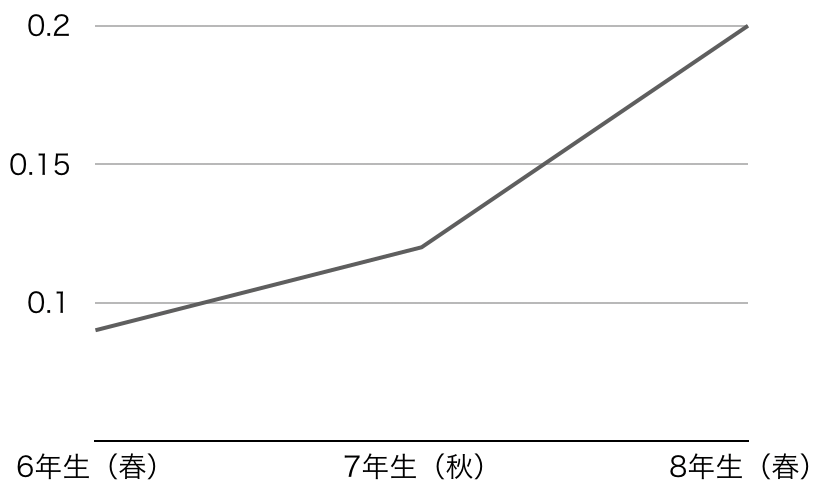
このように、暗黙の知能観と成績の相関係数は、6年生の春学期の.09(有意ではない)から、7年生の秋学期の.12(p<.05)、8年生の春学期の.20(p<.05)というように上昇していきます。
さらに、回帰分析(因果関係の分析)で、7年生のはじめの暗黙の知能観は、8年生の終わりの成績と強い因果関係にあることが分かりました(β[回帰係数]=.17, t=3.40, p<.05)。
因果関係とは、「AがBの原因である」という関係です。つまり、暗黙の知能観と成績に正の因果関係があるということは、「暗黙の知能観が良い学業成績をもたらす」ということです。これは、同時に「BがAの原因である」ということではありません。つまり、良い学業成績がより強い暗黙の知能観をもたらすということではありません。あくまでも「A(暗黙の知能観)がB(良い成績)の原因」です。
さらに、6年生の時の数学のテストの点数を、統計的に調整した上(分析項目の中の不純な要素を除外した上)での分析では、強い因果関係が認められます(β=.43, t=8.48, p<.05)。また、回帰分析において、6年生の春学期のテストの点数ではなく、7年生の秋学期の数学の成績を使った場合、暗黙の知能観と成績に、非常に強い因果関係が認められます(β=.70, t=17.50, p<.05)。
これはつまり、中学、高校、大学、社会というように、状況が困難なものになればなるほど、暗黙の知能観(能力は努力や訓練によって伸びる)の信念を持つ人たちの方が、より大きな業績を達成することを表します。
1.3.3. 暗黙の知能観と成長カーブの関係
さらに、暗黙の知能観(能力は努力と訓練によって伸ばせる)の信念が高ければ高いほど、成績の成長カーブ(その後の伸び方)が大きくなる(因果がある)ことがわかりました。
念のため、方程式の話をしておきます。統計に明るくない場合や、さほど興味がない場合は、理解できなくて全く問題ないですので、次の画像(Figure2)が出てくるところまで読み飛ばしてください。
この成長カーブの分析においては、ブリュックとローデンブッシュが『変化を計測するためのヒエラルキー的線形モデルの応用』、『社会科学における上級定質テクニックⅠ:ヒエラルキー的線形モデル:応用とデータ分析メソッド』の階層的線形モデル(HLM)を使っています(※3,4)。
以下がレベル1の方程式です。
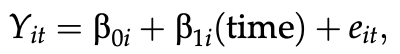
β0は切片、つまり、Time1の数学の平均成績です(7年生の秋学期がtime1、春学期がtime2、8年生の秋学期がtime3、春学期がtime4とコードされています)。β1は傾き、つまり学期(time)単位の成績の平均変化です。数学の成長カーブは4つの学期の成績を繋ぐことで作成しています。
レベル2の方程式では、これに暗黙の知能観スコアを加えていきます。
なお成長カーブを算出する前に、4つのグループの潜在的差異が調整(分析に狂いを起こす不純要素として排除)されています。具体的には、この研究では、別のグループの生徒たちは、別の教師から学んでいます。そのため、教師の違いによって、評価の付け方や、教師自身の教え方の有効性に、微妙に違いがある可能性があります。
そのため、以下のように、それぞれのグループの方程式にダミー変数を組み込んでいます。
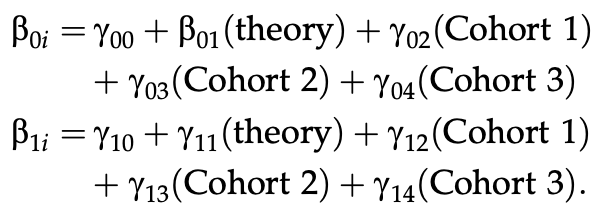
このように、グループのダミーを入れることで、それぞれのグループ間の潜在的な差異を調整した、平均成長レベルを見積もることができます。
こうして成長カーブをグラフ化したのがFigure2.です。
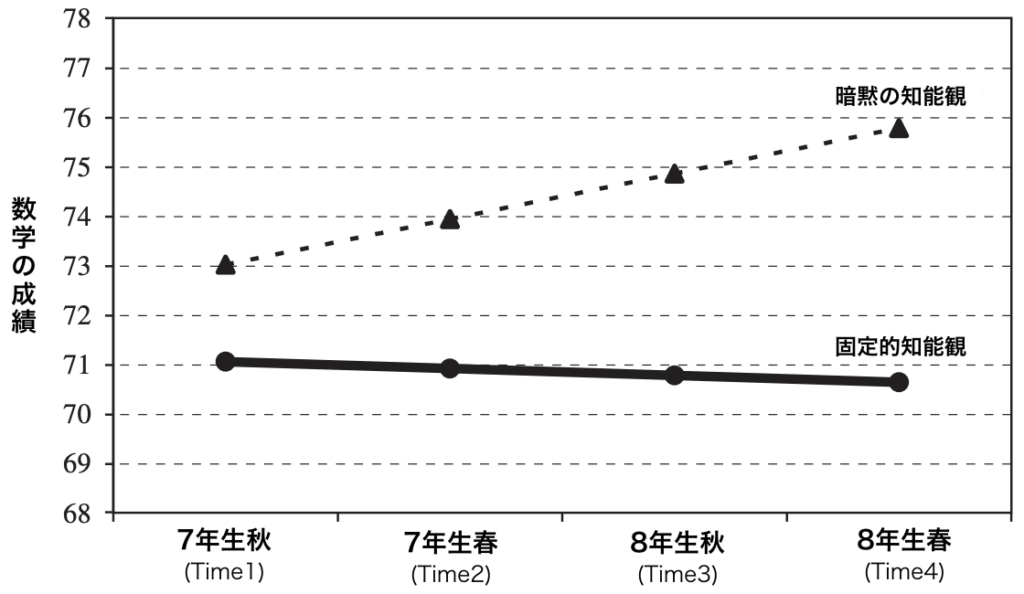
Time1の平均成績は72.05(C-評価)でした。この時点では、知能観と成績に有意な因果関係は見られません(β=.98, t=1.47, ns) 。しかし、Time2 以後は、暗黙の知能観と成績の成長カーブの間に、因果関係が顕著に見られました。(β=.53, t=2.93, p<.05) 。
この結果は、暗黙の知能観の信念が強くなるほど成長カーブが急になる、ということを意味しています。
なお、Figure2.は、エイケンとウェストの『重回帰分析:相互効果のテストと解釈』のガイドラインにしたがって、知能観の平均に対して上下に1の標準偏差スコアを用いています(※5)。
以上の3つの結果は、暗黙の知能観が、各種モチベーションを増大させ、その結果として成績が良くなることを示しています。
つまり、成績の向上をもたらすのはモチベーションであり、モチベーションの向上をもたらすのは、暗黙の知能観(能力は努力と訓練によって伸ばすことができるという信念)であるということです。暗黙の知能観が、良い成績と因果関係にあるということは、こういうことです。
具体的には、知能観は、中学生に移行した時の数学のテストの点数に対しては関係はありませんでした。しかし、その後の2年間で、学業の困難さが増していくほど、暗黙の知能観の生徒たちと固定的知能観の生徒たちの間で、成績が大きく乖離していきました。
そのことから、困難な状況になればなるほど、より良い成績や業績を達成する為に高いモチベーションが必要になる、つまり、高いモチベーションをもたらす要因である暗黙の知能観が重要だということです。
人生は困難の連続ですが、それを乗り越えるための出発点が、暗黙の知能観(能力は努力と訓練によって伸びるという信念)なのです。
1.4. モチベーション経路モデル
当研究の目的は、暗黙の知能観と成績の関係を記録するということを超えて、なぜ暗黙の知能観がより良い成績をもたらすのか、という仕組みを解明し、モデル化することです。そのために、構造方程式モデリング(SEM)という解析を行います。
1.4.1. 暗黙の知能観がモチベーションを高め、成績を高める仕組み
まずは結果から見ていきましょう(Figure3)。
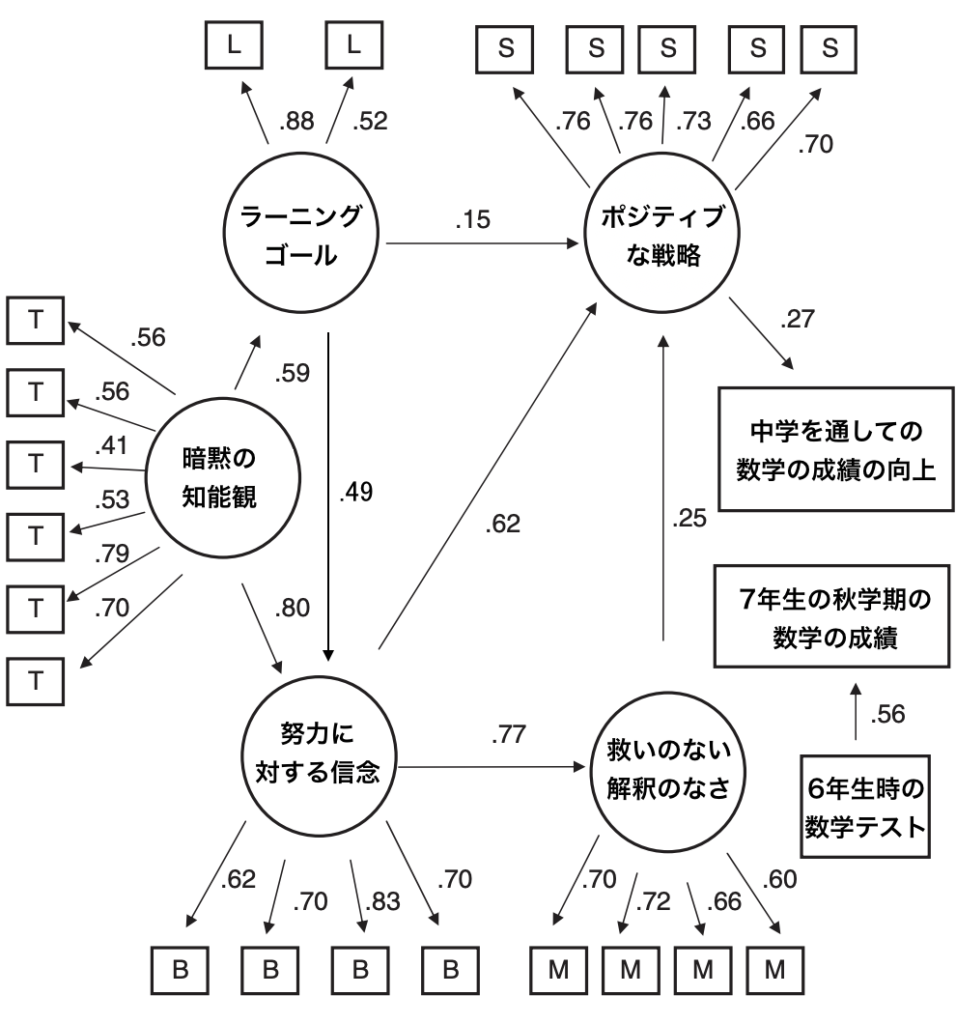
モデルは、データと十分にフィットしているものとなりました。つまり数学的に正確性を保証できるものだということです(X2=6,044.23; df=291; p<.05; CFI=.92; RMSEA=.06; p close fit 5 .03)。
なお、モデル内の数字はパス係数です。パス係数とは、回帰係数のようなもので、上限を1.0として数値が高ければ高いほど、矢印の先の観念を形成する原因となっていることを示します。
それではモデルについて解説します。
まず、暗黙の知能観(能力は努力と訓練によって伸びるという信念)が、ラーニング・ゴール(.59)と努力に対するポジティブな信念(.80)を形成します。
次に、ラーニング・ゴールは、努力に対するポジティブな信念(.49)、困難な状況においてポジティブな戦略を模索する姿勢を形成します(.15)。
続いて、努力に対するポジティブな信念は、困難な状況において救いのない解釈(現実逃避)をせずに現実に立ち向かう姿勢(.77)、困難な状況においてポジティブな戦略を模索する姿勢(.62)を形成します。
そして、困難な状況において救いのない解釈(現実逃避)をせずに現実に立ち向かう姿勢は、困難な状況においてポジティブな戦略を模索する姿勢(.25)を形成します。
最後に、ラーニング・ゴール、努力に対するポジティブな信念、困難な状況において救いのない解釈(現実逃避)をせずに現実に立ち向かう姿勢のそれぞれの影響によって形成された、困難な状況においてポジティブな戦略を模索する姿勢は、中学の2年間を通してのより良い成績を生み出します。
これが、暗黙の知能観が、モチベーションの向上をもたらし、結果的に成績の向上をもたらす仕組みです。
1.4.2. モデル化における統計的な面での補足
構造方程式モデリングについて補足をしておきます。こちらについては、小難しい話なので、次の見出しまで読み飛ばして頂いても問題ありませんから、ご安心ください。
さて、モチベーション経路のモデル化については3つのアプローチを使いました。
まず、4つのモチベーションの構成要素(ラーニング・ゴール、努力に対する信念、救いのない解釈[逃避行動]の少なさ、ポジティブな戦略)を一つの要因(以下、「モチベーション」と呼ぶ)として、それが、知能観と成績の関係の媒介役となるかを見ました。つまり、「暗黙の知能観が、モチベーション全般を向上させ、モチベーション向上が成績の向上をもたらす」、という仮説が正しいのかどうかの確認です。
次に、4つのモチベーションの構成要素(ラーニング・ゴール、努力に対するポジティブな信念、救いのない解釈の低さ、ポジティブな戦略)が、それぞれ、成績向上をもたらす独立した一つ一つの変数として機能するかどうかを検証しました。
最後に、これらの2つを組み合わせて、モチベーション経路モデルが数学的に妥当なものであるかどうかを検証しました。
それぞれの結果は次の通りです。
まず、モチベーションの構成要素の全てを、探索的因子分析にかけて、回転のない因子を記録しました。結果、努力に対する信念の12項目のうち3つと、ラーニング・ゴールの4項目のうち1つ以外の、全ての要素の因子負荷量は.30以上でした。これらの要因は、知能観と学業成績の相関関係の31.79%を説明するものとなり、高い寄与率を示しました。
そして、モチベーションが、暗黙の知能観と成績の変化の媒介変数であるかどうかをテストしました。結果、総合モチベーションは、有力な媒介変数であることがわかりました。この探索的因子分析の結果、暗黙の知能観と数学の成績の相関係数は、.20から.11に有意に減少しました(p<.05)が、モチベーションと成績の相関係数は.19(p<.05)でした。
この結果から、暗黙の知能観が、モチベーションを向上させ、モチベーションの向上が、数学の成績を向上させる、という仮説が正しいことが分かりました。
次に、構造方程式モデリングを使い、全ての潜在変数が自由に共変できるモデルを検証しました。
モデリングにおいて、暗黙の知能観は3つの固定的知能観と3つの暗黙の知能観(反転した点数)のアンケート項目のスコアが入力されています。ラーニング・ゴールは3つのラーニング・ゴールのアンケート項目のスコアが入力されています。
努力に対するポジティブな信念は、4つに分類した上で入力しました。そのうち3つはポジティブ(反転した点数)とネガティブを1つ含むものがランダムに組み合わされたもので、4つ目はポジティブ(反転した点数)を1つ、ネガティブを2つ含むものです。(注:このようにアンケート結果を分類して分析にかける方法を「パーセリング」と言いますが、これについては、キシュトンとウィダマンの『アンケート項目の表面的対領域代表的パーセリング:実証的例』が参考にされています ※6)。
救いのない解釈の低さは4つの項目を、ポジティブな戦略は5つの項目を入力しています。2年に渡る数学の成績の成長カーブが、結果変数として使われています。
まず、この測定モデルは、十分にデータとフィットしていました(X2=517.47, p<.05, df=253, CFI=.94, RMSEA=.05, p=.22)。修正インダイスが、戦略スケールの「より時間をかける」、知能観スケールの「新しいことを学ぶことはできるが、基本的な知能を変えることはできない」「現在の知能がどうであっても、いつでも伸ばすことができる」の3つを、ラーニング・ゴールの要因に修正するように提案しました。しかし、これらの負荷量の大きさは、他のラーニング・ゴール項目よりははるかに小さなものだった(all<.17)ので、そのままにして分析が進められています。
次に、このモチベーション・モデルのフィットをテストしました。結果、このモデルは、暗黙の知能観が、努力に対するポジティブな信念とラーニング・ゴールを育み、それによって救いのない解釈の減少、ポジティブな戦略の採用に繋がり、結果、成績が向上するという経路を特定しました。
最後に、OLS回帰分析とソベルテストを用いて、それぞれのパス係数を検証しました。ラーニング・ゴール、努力の信念(2回)、救いのない解釈、ポジティブな戦略(3回)の7回のテストが行われました。全てのテストが、どのパス係数も重要であることを示しました(zs ranged from 2.14 to 8.56, ps<.05)。
1.5. 実験1のまとめ
まとめると、実験1は、現実世界での達成を左右するモチベーション経路モデルが有効であることを証明してくれました。「能力は努力と訓練によって伸ばすことができる」と信じる中学生の生徒たちは、「能力は生まれつき決まっている」と信じる生徒たちと比べて、より強くラーニング・ゴールになり、より強く努力に対するポジティブな信念を持つようになりました。
そして、ラーニング・ゴールとポジティブな努力の信念を持つ生徒たちは、挫折や失敗などの困難な状況に直面した時に、能力のせいにして現実逃避する傾向(救いのない解釈の傾向)が、見られませんでした。
これらの信念をもつ生徒たちは、挫折や失敗を、能力不足のせいにして、無気力になるようなことはせずに、それらは、もっと戦略の変更の必要性や、努力の必要性を伝えてくれる機会であると認識します。
こうした困難な状況における反応パターンの違いは、生徒たちの実際の成績に反映されています。約2年後、中学入学時に強い暗黙の知能観を持っていた生徒たちは、より固定的知能観を持っていた生徒たちの成績を顕著に上回ったのです。
